How To Calculate & Determine Measurement Uncertainty?

When checking whether a part’s dimensions match the drawings, measurements must always be taken. But have you ever wondered how accurate those measurement results really are?

You might think results from an expensive measurement device are correct. However, there is always some uncertainty in measurement results. And this uncertainty is not inherent in the measurement device itself, but rather attached to the measurement results.

In other words, even when using the same measurement device, the uncertainty will vary depending on measurement conditions, environment, the person doing the measurement, and other factors.

If measurements are taken without understanding uncertainty, the measurement uncertainty tends to increase. With high measurement uncertainty, the results will vary significantly each time a measurement is taken, or deviate far from the true value. This can lead to an inability to ensure the part’s quality.

Therefore, understanding measurement uncertainty is crucial for ensuring part quality through measurements. Recognizing and managing uncertainty is key to obtaining reliable, meaningful measurement results.

What is Measurement Uncertainty?

Measurement uncertainty is a quantitative expression of the ambiguity of the measured value. This ambiguity arises from variations in the measurement data and imperfections in the information used for measurement itself. Paradoxically, indicating the ambiguity of the measured value clarifies the reliable range of the measured value. If you measure the same test body repeatedly, slightly different values will appear each time. The measured value is one sample value among them. Variations that cannot be fully corrected by the measuring instrument are also factors of measurement uncertainty. To indicate how reliable a measurement value is, an index representing the variation range, that is, measurement uncertainty is needed.

Why is Measurement Uncertainty Needed?

Measurement uncertainty information is required when some kind of judgment is needed based on measurement values. For example, consider a test related to human health and safety where the specification has an upper limit and the performance of the product being tested must not exceed that limit. This will be easily understood from examples such as BSE inspection or measurement of asbestos content. It is quite common to re-measure values that are close to the upper limit. This is because it is known that there is variability in measurement values and measurement objects. Judgment becomes easier if the extent of variation in measurement values is understood, since it allows judgment including the variation range.

Why Does Measurement Variation Occur?

Measurement results inherently have variation. There are various causes of variation, but random effects such as short-term fluctuations in temperature, humidity, air pressure during measurement, or the skill level of the measurer can be considered. There are also systematic effects such as the accuracy of the measuring instrument or bias when people read values. Variation in measurement values occurs due to these effects.

It is also possible that the same value is measured repeatedly without variation, which means the measurement does not require high precision and the instrument accuracy is not enough to show variations. Conducting more precise measurements would reveal that measurement values inherently vary due to the properties of measurement.

Importance of Measurement Uncertainty

In the past, “error” was used to express the correctness of measurement results. Now, the concept of “uncertainty” is more commonly used.

Uncertainty quantifies how reliable a measurement result is numerically. For example, 99.95 mm ± 0.10 mm (confidence level 95%) means:

99.95 mm is the measurement result
0.10 mm is the uncertainty
There is a 95% probability the true value is between 99.85-100.05 mm

Expressing uncertainty clearly shows the probability and range that the true value exists within. This is important for demonstrating measurement reliability.

Uncertainty allows more accurate pass/fail judgments of part dimensions. It can identify potential out-of-tolerance issues that may not be caught without uncertainty data.

International Rules of Measurement Uncertainty

The WTO/TBT agreement (Agreement on Technical Barriers to Trade) aims for the free flow of goods and services internationally by adopting a set of compatible assessments internationally as international rules, and each country also agrees to this. ISO 9001 is a requirement for general business quality management systems, and similar requirements are established as ISO/IEC 17025 to manage quality of testing at testing bodies. It includes provisions for equipment management and tester training when using instruments for measurement, and measurement uncertainty must be evaluated according to ISO/IEC 17025 and reported along with test results attached to reports.

Measurement Uncertainty Calculation: How To Calculate & Determine Uncertainty of Measurement?

Uncertainty comes mainly from “bias” and “variation”:

Bias is the difference between the true value and average measured value. It can cause results to be consistently too high or low. Corrections can reduce bias uncertainty.

Variation describes the spread of measurement results. It happens randomly so cannot be corrected. Variation comes from measurement conditions, instrument precision, operator skill etc. Improving these aspects reduces variation uncertainty.

Key Steps To Calculate uncertainty (called estimation):

Identify all potential uncertainty sources
Calculate/measure the uncertainty contribution of each source (ui)
Only include significant sources
Combine using the root-sum-of-squares to get combined standard uncertainty (u)

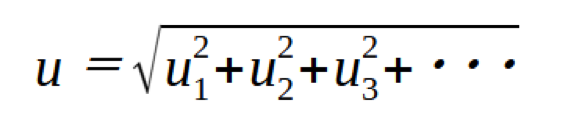
There is no correct answer regarding the number or type of uncertainty factors. It is OK if you list just the right amount. Because of the self-reporting system, companies without technical capabilities cannot think of the causes of uncertainty and tend to reduce uncertainty. However, if the uncertainty is smaller than the actual ability, it is called an “underestimation” and loses social credibility. Care must be taken not to underestimate uncertainty.

Coverage Factor Indicates Confidence Level

A coverage factor k (e.g. k=2) on a measurement device indicates the level of confidence in the estimated uncertainty.

k=2 corresponds to a 95% confidence level. The expanded uncertainty U is calculated as U = ku.

Proper uncertainty evaluation requires traceability and is important for advanced manufacturing and quality control. Standards are increasingly requiring uncertainty analysis.

Methods for Evaluating Measurement Uncertainty (GUM Method)

ISO has provided guidelines for evaluating measurement uncertainty, which has been translated into Japanese. This guideline is called GUM and adopted in various fields of measurement. The procedures for evaluating measurement uncertainty using the GUM method are as follows:

STEP 1: Define the measurand

The measurement target is called the measurand. Evaluation of measurement uncertainty starts with expressing the measurand in an equation. The measurand is generally expressed by several components, i.e. y=f(x₁,x₂,…). Here, y is the value of the measurand and x are the values of components. Some examples of defining the measurand are:

Compressive strength of concrete: F=P/A (F is compressive strength N/㎟, P is load N, A is cross-sectional area ㎟)
Density of building material: ρ=M/V (ρ is density kg/m³, M is mass kg, V is volume m³)

STEP 2: Estimate the standard uncertainty of each component

Estimate the magnitude of variation for each component shown in the definition of the measurand. Components also consist of several factors. For example, variation obtained from repeat observation, variation due to temperature fluctuations, variation due to errors in measuring instruments, etc. Evaluation based on repeat observation is called Type A evaluation, and other methods are called Type B evaluation. The magnitude of variation for each factor is expressed by the standard deviation or equivalent quantity, and the square root of the sum of their squared values is called the standard uncertainty of that component.

STEP 3: Combine standard uncertainties

Combine the standard uncertainties of each component to obtain the standard uncertainty of the measurand. The method of combination is the square root of the sum of squares, but since the dimensions of components and measurands are different, the following propagation of uncertainty formula is used:

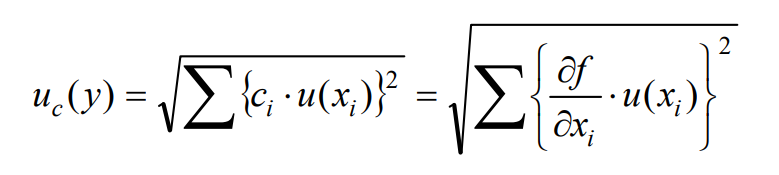
Here, u_c(y) is the combined standard uncertainty, and c_i is the sensitivity coefficient of component i. The sensitivity coefficient is expressed as the partial differential of a measured quantity with respect to a certain component, and means the rate of change in the measured value when that component changes slightly.

STEP 4: Calculate the expanded uncertainty

The combined standard uncertainty estimates the variation of measured values, meaning the standard deviation of its distribution. To express the variation with a higher confidence level, the expanded uncertainty U is calculated by multiplying the combined standard uncertainty by a coverage factor k: U=k x u_c(y). The value of k is selected in the range of 2-3 depending on the confidence level.

STEP 5: Express measurement uncertainty

The measurement result is expressed along with the measurement value and expanded uncertainty. For example, density ρ=1.23kg/m³±0.12kg/m³ (k=2). The number following ± is the expanded uncertainty. A value of k=2 generally corresponds to a 95% confidence level.

Measurement Uncertainty is a relatively new concept, so we think there are many workplaces that haven’t adopted it yet and many bosses who don’t know about it.

However, the importance of uncertainty is becoming more widespread around the world, and standards such as ISO are being developed.